HeatMap Profession ~ Parti des candidats aux élections législatives et contribution au khi-deux (suite)

Dans le précédent post, nous avons déjà vu quelques notions permettant d'analyser le lien entre la profession exercée par les candidats aux élections législatives et leur appartenance politique.

Nous aurions pu compléter l'analyse des correspondances grâce à une petite heatmap montrant les effectifs et leur aspect significatif..

Plan:

• La HeatMap
• Calcul du khi-deux, explications
• Les éléments-clé du code
• Le code complet sous github

La heatmap

Dans cette heatmap, l'intensité de la couleur est relative à la valeur du khi-deux de la cellule (issue du couplage de deux modalités, Profession et Parti). Plus la valeur est élevée entre ces deux modalités et plus leur correspondance est élevée.

Nous avons superposé les effectifs pour une meilleure compréhension.

Un effectif faible peut être associé à une valeur de khi deux élevée. Dans ce cas, cela indique que la faiblesse des effectifs est caractéristique du couplage des deux modalités.

On peut prendre l'exemple de quelques cellules du tableau...

• L'effectif associé au couple Avocat - UMP est élevé de même que la valeur du khi deux. Cela indique que les candidats qui exercent le métier d'avocat sont davantage d'UMP.
• On peut faire une observation similaire entre Ouvrier et Extrême-Gauche.
• Pas mal de candidats fonctionnaires de catégorie A sont socialistes.
• On a une valeur de khi deux élevée pour le duo Cadre Supérieur dans le privé et Extrême-Gauche mais un effectif faible, ce qui semble indiquer que, de manière significative, il y a très peu de candidats cadres supérieurs qui représentent ce parti.
• Aussi, on voit que pour ce qui est des candidats écologistes, on retrouve beaucoup la catégorie "autres professions libérales". S'agit-il de professions libérales non réglementées ou réglementées? Dommage que l'on n'ait pas plus de détails car c'est véritablement pour cette catégorie d'activité professionnelle que le parti Ecologiste est le mieux représenté.

Attention, ceci est seulement mon interprétation des résultats et peut être sujet à observations, critiques, notamment sur la méthode statistique employée. N'hésitez pas à commenter.


Calcul du khi-deux, explications

Pour savoir si un lien est fort entre deux modalités, il faut savoir si l'effectif les réunissant est caractéristique. Pour cela, on prend en compte son "environnement" en lignes et colonnes dans le tableau de contingence. Si l'effectif est fort et si les effectifs des cellules en lignes, d'une part, et en colonnes, d'autre part, sont élevées, alors l'effectif fort n'est pas vraiment caractéristique du couple de modalités. Le contraste n'est pas assez fort.

Afin de pouvoir quantifier le côté caractéristique d'un effectif croisant deux modalités, il faut prendre en compte les effectifs marginaux en lignes et colonnes relatifs à cette valeur. Ceux-ci correspondent aux effectifs relatifs à chaque modalité du couple en lignes et colonnes. Il faudra aussi prendre en compte l'effectif total afin de raisonner à une échelle globale, l'échelle du tableau de contingence.

La valeur du khi-deux au niveau d'une cellule d'un tableau de contingence est la suivante:

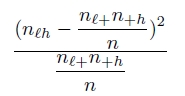http://www.math.univ-toulouse.fr/~baccini/zpedago/asdm.pdf

• nlh est l'effectif au sein de la cellule du tableau
• nl+ est l'effectif marginal en lignes. Si les professions sont en lignes, cela correspond au nombre de candidats exerçant la profession considérée.
• n+h est l'effectif marginal en colonne.
• n est l'effectif total, soit le nombre de candidats

La somme des khi-deux partiels des cellules donne la valeur du khi deux, totale.

L'illustration ci-dessous montre les différentes valeurs de khi deux obtenues pour différents environnements lignes et colonnes au niveau d'une cellule:

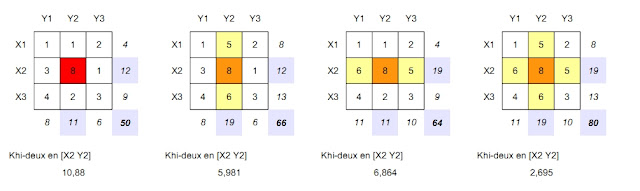schéma fait maison montrant la valeur du khi deux en une cellule (les cellules environnantes dont les valeurs ont changé sont en jaune)

Dans le premier tableau, la valeur du khi-deux vaut:

(8-(12*11)/50)² / (12*11)/50

La valeur du khi-deux décroît à mesure que les valeurs environnantes approchent celles de la cellule.



Les éléments clés du code

Lecture du fichier Excel

Pour lire le fichier excel des législatives, j'utilise la librairie gdata. La deuxième feuille comprend le tableau de correspondances entre code des partis (encore appelé nuance) et libellé de ces derniers.

f <- read.xls("IN/Leg 2012 Candidatures T1 31 05 2012.xls", sheet=1)
nuances <- read.xls("IN/Leg 2012 Candidatures T1 31 05 2012.xls", sheet=2, skip=2, header=FALSE)

Reshape Casting

Comme mentionné dans le post précédent, l'obtention du tableau de contingence a nécessité un reshaping de la donnée initiale en basculant les partis en colonnes. Cela se fait avec la fonction cast de la librairie reshape

f$value <- 1
r <- cast(f[, c("Profession", "NuanceLib", "value")], Profession~NuanceLib, sum)

Fonction de calcul du khi-deux

J'ai réalisé une fonction permettant de calculer le khi deux au sein de chaque cellule du tableau et obtenir une matrice de contribution au khi-deux.

khideux <- function(mat){
  m.cont <- mat
 
  sumR <- apply(mat, 1, sum)
  sumC <- apply(mat, 2, sum)
  sumT <- sum(mat)
 
  for (i in 1:nrow(mat)) {
    for (j in 1:ncol(mat)) {  
      w <- (sumR[i]*sumC[j])/sumT
      khikhi <- (mat[i, j] - w)^2/w
      m.cont[i, j] <- khikhi
    }  
  }
  return (m.cont)
}
 
m.cont <- khideux(r.m)

HeatMap 

Il existe une fonction native dans R appelée heatmap. Elle n'a pas été utilisée ici car je n'ai pas trouvé de moyen de spécifier les points de cassure pour les couleurs (break= ). J'ai donc utilisé la fonction image qui permet de paramétrer de manière plus fine la représentation graphique d'une heatmap.

image(t(m.cont2), breaks=cls$brk, axes=F, col=pal(20))

Libellés

Pour les libellés, il a fallu tout d'abord que je détermine la position/les coordonnées de chaque label au sein du tableau. Pour un tableau de 3 colonnes et 2 lignes, la séquence de coordonnées est la suivante pour les x: 123 123 et pour les y: 111 222. Les cycles sont différents. Dans le deuxième cas, on utilisera each, dans le premier non.

xs <- seq(0, 1, length.out=ncol(r.m))
ys <- seq(1, 0, length.out=nrow(r.m))
 
xs2 <- rep(xs, nrow(r.m))
ys2 <- rep(ys, each = ncol(r.m))

Puis ensuite, j'ai pu procéder à leur affichage

text(xs2, ys2, labels=ifelse(v>0, v, NA), col=gray(.5), cex=fsz*.6, font=2)

Le code sous gihub