Le bâti de Paris façon réseau ou comment faire des gribouillis avec R comme avec Processing

Paris sous forme de réseau. Non, on ne parle pas de rues, mais de bâti. Dans cet article, nous proposerons le passage d'une représentation à plat des bâtiments en une figuration sous forme de lignes, aux multiples évocations. On verra qu'avec R, on peut faire certaines choses comme Processing, l'outil de référence en design génératif.

La carte

Cliquer sur l'image pour la voir en grand sur flickr

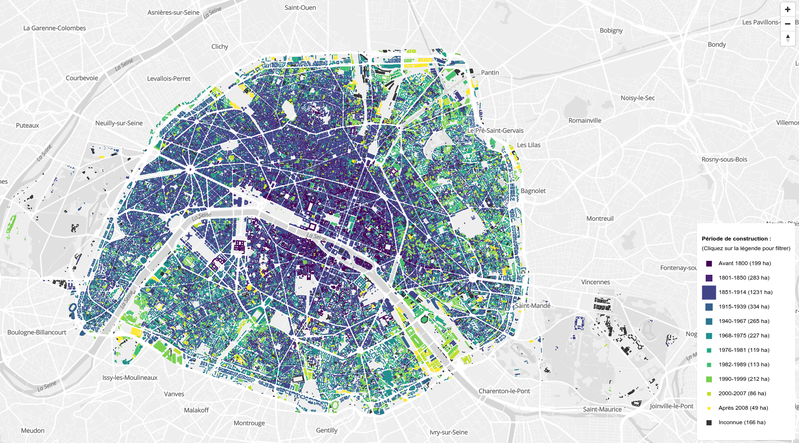
Sur cette carte est représenté le bâti de Paris sous la forme d'une toile. Chaque point de couleur représente un bâtiment et la couleur de chacun indique la période de construction du bâtiment. 

La rampe de couleurs est celle utilisée par Etienne Côme sur sa carte interactive BATIPARIS.

Sur ma carte, un arc relie deux bâtiments et il est d'autant plus clair qu'il relie deux bâtiments de périodes de construction différentes.

Ce mode de visualisation peut être intéressant pour explorer les différences de valeur dans une variable dans un voisinage, comme dans le cas de cette carte de la densité de population en France :

Différence de densité de population au niveau départemental (RGP INSEE 2013)

Sur ma carte, en suivant le réseau, on trouve toujours un chemin pour aller d'un bâtiment à un autre, même si l'on part de la place de l'Étoile pour se diriger vers Bercy; ceci a été obtenu grâce à une technique appelée arbre couvrant de poids minimal. Cette représentation a pour objet d'illustrer la densité d'une ville où tout serait interconnecté.

Paris dresse sa toile

La représentation du bâti est le plus souvent faite avec l'emprise des bâtiments, ce qui peut donner de beaux résultats comme celui de BATIPARIS.
Afin d'illustrer l'évolution champignonnesque d'une ville et se départir de cette représentation classique des bâtiments, on pourrait être tentés de représenter cela sous forme de réseau.

toile d'araignée, mycélium et réseau neuronal

Sur ma carte, les ramifications qui relient chaque bâtiment peuvent évoquer de multiples choses : les synapses de neurones rappelant les smart cities, les filaments d'un mycélium, voire même, si on regarde tout ça en noir et blanc, une sorte d'écriture qui évoquerait le tissage, au fil du temps, d'un tissu urbain.

Les données

Les données utilisées sont celles de l'Atelier Parisien d'URbanisme (APUR). Les données de bâti de l'APUR sont très riches. Outre la période de construction, on y trouve l'année de réhabilitation, les caractéristiques de la toiture, la surface d'ensoleillement,...
Une variable est particulièrement intéressante, que nous exploiterons peut-être dans un nouveau post : la hauteur des bâtiments.



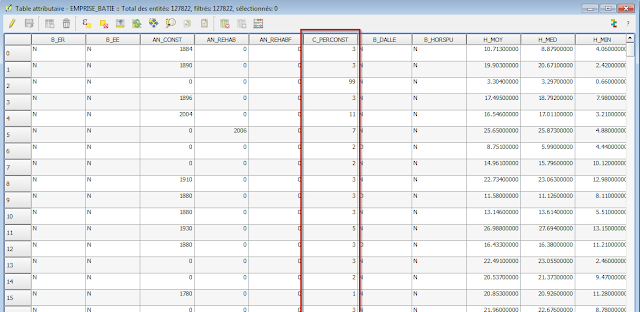
La colonne que nous avons utilisée est la même que celle utilisée par Etienne Côme dans son application : la colonne C_PERCONST.

La transformation

L'illustration ci-dessus, créée par Benedikt Gross, montre le processus en cours lors d'un design de données. Je lui ai juste ajoutée les outils utilisés.
Pour obtenir notre carte, nous avons créé un algorithme exploitant la théorie des graphes ainsi que des techniques de design génératif. Pour ce dernier domaine, Processing constitue l'outil de référence. Il est adopté par nombre de data artists, d'artistes multimédia. Nous verrons grâce à cet article que R permet aussi de faire du design génératif. Néanmoins, pour peindre nos données, nous nous sommes tournés vers un second outil : QGIS, plutôt que R, en raison de capacités graphiques assez particulières.

Dans un premier temps, les centroïdes des bâtiments ont été générés

L'île de la Cité

Ensuite, nous avons relié tous ces points grâce à la fonction de Delaunay

De l'eau naît

J'ai trouvé que le nombre de segments était bien trop grand pour le rendu final. Afin de l'épurer, j'ai utilisé une technique de la théorie des graphes appelée Arbre couvrant de poids minimal, ou minimum spanning tree en anglais. Cet arbre est tel qu'on peut trouver un chemin entre chaque sommet avec un nombre de branches minimal

MST (Minimum Spanning Tree)

Les liaisons entre bâtiments étaient selon moi trop rectilignes. Afin d'obtenir quelque chose de plus "smooth", j'ai utilisé les courbes de Bézier. C'est une forme visuelle très usitée dans les infographies de réseaux.

Avec Bézier, tout devient plus doux

Le style

• J'ai adopté un fonds noir pour mettre en contraste les données. 
• J'ai posé le réseau de segments avec un petit effet flou, avec le mode de fusion "addition" et une valeur de luminosité différente selon la différence de période reliant deux bâtiments. Grâce au mode addition ajouté entre les objets, les endroits où les segments se superposent semblent s'éclairer.
• Par-dessus, j'ai posé les centroïdes de bâtiments coloriés selon la période de construction, avec un mode de fusion "revêtement". Pour rappel, la rampe de couleurs est celle utilisée dans BATIPARIS. J'avais utilisé le mode de fusion "revêtement" pour la carte de l'orientation des rues de Paris. Avec ce mode, c'est comme si on teintait une couche avec les couleurs d'une autre.
• Enfin, en dessous, j'ai disposé la Seine afin de donner un contexte. Celle-ci se trouve dans une couleur hors du spectre utilisé pour le bâti, et avec un peu de flou pour donner un côté organique et en atténuer la présence. 

J'aurais pu rajouter des données contextuelles supplémentaires mais j'ai préféré garder un côté minimaliste pour cette carte.

Voici un tableau récapitulant l'agencement des différentes couches dans QGIS avec leur style et leur ordre de superposition :

Variations

J'ai réalisé des petites variations autour de cette carte.

Tout d'abord, en générant des lots de données par période, on peut voir dans quelles zones Paris a dressé sa Toile au cours du temps. C'est comme si on voyait la signature de chaque époque.

Jusqu'en 1800, on construit surtout au centre

Georges Eugène Hausmann est dans la place. Ca construit à tout va, y compris des places (comme celle de l'Étoile)

Le rythme de construction semble plus modéré dans les 80's, à part peut-être dans le NE de la capitale

Le code

Décortiquage

La librairie spdep a permis de réaliser la triangulation de Delaunay :

coords = coordinates(ile_cite)
nb = tri2nb(coords)

ainsi que de calculer l'arbre couvrant de poids minimal :

nb = tri2nb(coords)
nbw = nb2listw(nb, zero.policy = FALSE)
mst.bh <- mstree(nbw,5)

J'ai créé une fonction appelée MakeLineFromCoords qui permet de tracer une ligne à partir d'une série de coordonnées. D'ailleurs, je me suis dit qu'elle pouvait être utile pour superposer tout type de graphique en ligne sur des cartes : par exemple, évolution du chômage par département au cours du temps :

makeLineFromCoords <- function(coords, i) {

  Sl1 = Line(coords)
  S1 = Lines(list(Sl1), ID=as.character(i))
  Sl = SpatialLines(list(S1))  
  return(Sl)
}

R inclut une librairie appelée bezier qui, comme son nom l'indique, permet de dessiner...des courbes de Bézier.

b = bezier(t=t <- seq(0, 1, length=100), p=rbind(coords[from, ], midpoint, coords[to, ]))

midpoint désigne le point d'ancrage situé entre les deux points à connecter. La position de ce dernier détermine la courbure finale de l'arc. J'ai injecté un peu de hasard dans la position de ce dernier.
Dans un premier temps, j'ai calculé la distance séparant les deux points :

d = sqrt((coords[from, 1] - coords[to, 1])^2 + (coords[from, 2] - coords[to, 2])^2)

Ensuite, j'ai bougé sa position selon certains seuils. Tout d'abord, j'ai calculé un facteur de transformation qui déterminera dans quelle direction se fait le déplacement du point :

ifelse(runif(1,-1,1) > 0, 1, -1)

Ensuite, j'ai appliqué un ratio tel que le point bougera dans un rayon allant du milieu situé entre les deux points à une distance égale au tiers de la distance séparant les deux points.

Voici le code correspondant au déplacement en X :

(coords[from, 1] + coords[to, 1])/2 + ifelse(runif(1,-1,1) > 0, 1, -1

Et celui en Y est similaire :

(coords[from, 2] + coords[to, 2])/2 + ifelse(runif(1,-1,1) > 0, 1, -1) * runif(1,0,d/3)

Au final, le point intermédiaire d'ancrage de la courbe de Bézier se situera ici :

midpoint = c((coords[from, 1] + coords[to, 1])/2 + ifelse(runif(1,-1,1) > 0, 1, -1) * runif(1,0,d/3),(coords[from, 2] + coords[to, 2])/2 + ifelse(runif(1,-1,1) > 0, 1, -1) * runif(1,0,d/3))

Le code dans son intégralité